Modelling of excitable cells - the EMI model

The Extra, Intral Membrane (EMI) model is a way of modelling the intracellular, extracellular and membrane between the two explicitly. A full introduction to the topic is given in [TMR21].

In this section, we limit ourselves two the following set of equations, with a single intra-cellular and extracellular space.

\[\begin{split} \begin{align*} -\nabla \cdot (\sigma_e\nabla u_e) &= f_e&& \text{in } \Omega_e\\ -\nabla \cdot (\sigma_i\nabla u_i) &= f_i&& \text{in } \Omega_i\\ \sigma_e\nabla u_e\cdot \mathbf{n}_e = - \sigma_i\nabla u_i\cdot \mathbf{n}_i &\equiv I_m&&\text{at } \Gamma\\ v &=u_e-u_i&& \text{at } \Gamma\\ \frac{\partial v}{\partial t} &= \frac{1}{C_m}(I_m-I_{ion})&& \text{at } \Gamma \end{align*} \end{split}\]

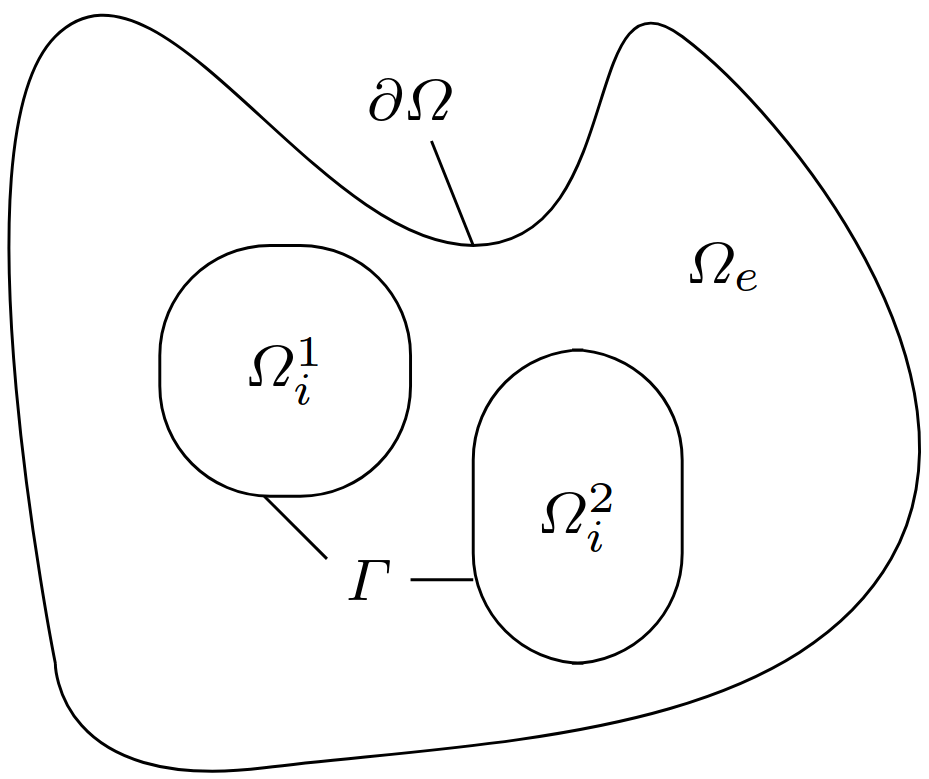
Fig. 1 Illustration of the intracellular and extracellular space. Figure is from [BFRSC24] and is under the creative commons license.

Implementations

With the fem, there are two classical ways of modelling Poisson-like equations, namely the primal and mixed formulation. However, as the EMI problem can be thought of as two Poisson problems with a specific coupling condition, it expands the number of possible discretizations to four [KMR21]:

• The primal, single dimensional domain formulation

• The primal, mixed dimensional domain formulation

• The mixed, single dimensional domain formulation

• The mixed, mixed dimensional domain formulation

References

[BFRSC24]

Pietro Benedusi, Paola Ferrari, Marie E. Rognes, and Stefano Serra-Capizzano. Modeling excitable cells with the emi equations: spectral analysis and iterative solution strategy. Journal of Scientific Computing, 98(3):58, Feb 2024. doi:10.1007/s10915-023-02449-2.

[KMR21]

Miroslav Kuchta, Kent-André Mardal, and Marie E. Rognes. Solving the EMI Equations using Finite Element Methods, pages 56–69. Springer International Publishing, Cham, 2021. doi:10.1007/978-3-030-61157-6_5.

[TMR21]

Aslak Tveito, Kent-Andre Mardal, and Marie E. Rognes, editors. Modeling Excitable Tissue: The EMI Framework. Springer International Publishing, Cham, 2021. ISBN 978-3-030-61157-6. doi:10.1007/978-3-030-61157-6.